Rian Architects & Designers
The purpose of this research is to apply the notion of fractal geometry in designing structural roof trusses. Fractal geometry, commonly characterized by the features of recursive self-similarity, is considered as a rule-based geometric system that can be generated by using the process of the Iterated Function System (IFS). Lattice configurations of conventional trusses generally show some extend of ‘self-similarity’ features that loosely and sometimes closely resemble with the properties of fractal shapes. The typical configurations of these regular trusses are strategically designed to provide adequate strength and stability to the structures for carrying enough vertical and wind loads. This paper, using the Iterated Function System based on Barnsely’s contraction mapping as a generative design method, proposes a new family of truss designs that follow the concept of fractal geometry. The Hausdorff dimensions and the Box Counting dimensions are evaluated to measure the fractality and detailness of the lattices of proposed fractal-based trusses. It also briefly investigates their mechanical properties for analyzing their practical feasibility in construction
FracTruss:
Fractal Based Trusses Design
Benoit Mandelbrot (1983) claimed in his seminal book The Fractal Geometry of Nature,
"My claim is that (well before Koch, Peano, and Sierpinski), the tower that Gustave Eiffel built in Paris deliberately incorporates the idea of a fractal curve full of branch points. … However, the A's and the tower are not made up of solid beams, but of colossal trusses. A truss is a rigid assemblage of interconnected submembers, which one cannot deform without deforming at least one submember. Trusses can be made enormously lighter than cylindrical beams of identical strength. And Eiffel knew that trusses whose 'members' are themselves subtrusses are even lighter.”
You also find me @
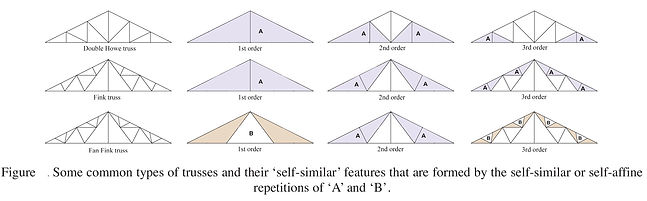
From a geometric point of view, when the internal configuration of a truss is designed by assembling the posts, diagonals and struts within the main frame, the foremost target is always structural, dealing with the compressions and tensions in the members to obtain the maximum stability and high stiffness, and in some cases, it considers the aesthetic appearances too. While the geometric constructions of the internal lattices of conventional trusses basically follows simple geometric rules, one striking feature, clearly recognizable in many examples, is the modular arrangement and repetition of simple geometric shapes at different scales. This repetition is meant for increasing the stiffness of the truss structure, by reducing the members slenderness. Generally, the more the repetitions are nested inside the truss frame, the more is the stiffness of the truss structure.
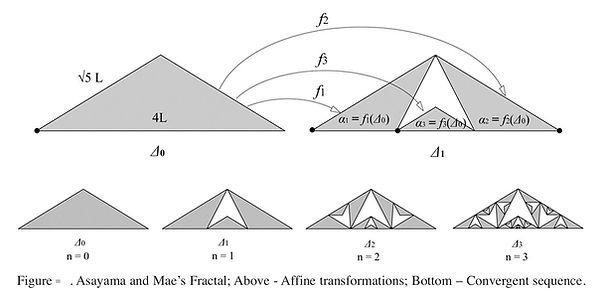
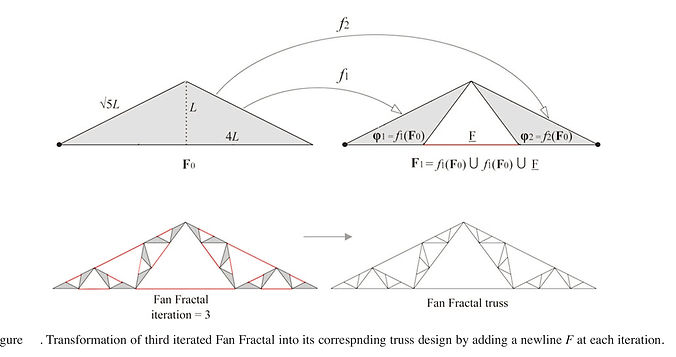

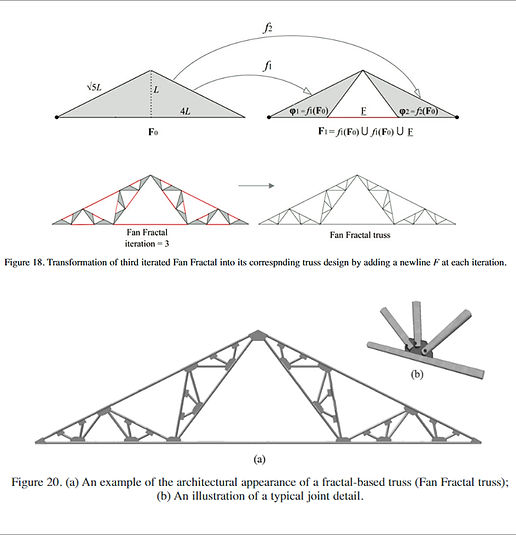
Fractal system has two important properties that are useful for structural design in the field of construction. The first property is that the fractal system can be expressed by using a simple algorithmic function. This property is useful for easily programming a fractal model in computer for designing structures. Second, fractal system is an assembly of some self-similar unit elements; hence, they form some hierarchical or modular system in structure. This property can be useful to construct long-span structures where modular units are required for stiffening and strengthening a structure. There are different methods to design a simple algorithmic function that can generate a fractal model. In this paper, Barnsley’s method (1988) of fractal construction is adopted which is based on his contraction mapping theorem and the Iterated Function System. Using his method and the principle of fractal geometry, some fractal models are constructed in this study in order to make different geometric configurations of some structural trusses. First two trusses are designed based on the well-known fractals such as Sierpinski triangle and Pinwheel Fractal, whereas other trusses are designed by reorganizing the configurations of traditional trusses using fractal rule. Asayama and Mae’s (2004) fractal truss is also included in this family of fractal-based trusses.
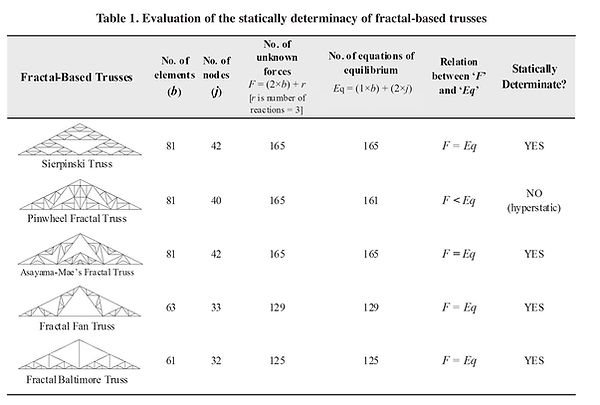
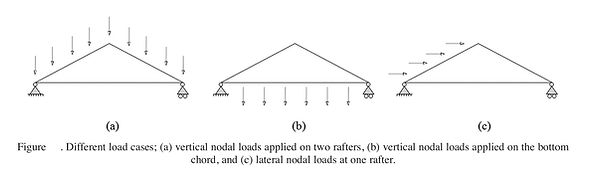
In order to have a first understanding of the mechanical behavior of the fractal-based trusses, a linear static analysis under various load conditions has been performed. Before the analysis, it is assumed that all members of the truss are perfectly straight, all joints are frictionless and all loads and reaction occur only at the joints. Since all the fractal-based truss models are statically determinate, except the Pinwheel Fractal truss model, the stiffness of members does not influence the distribution of internal axial forces, while it has an effect on the nodal displacements. Further, the self weight of the trusses is not taken into account, being usually much smaller than the other loads, so that a unique kind of cross section is adopted for all the bars that form the trusses. Because the self weight is also an indicator of the amount of steel required for construction, and then of the cost, using the same cross section for all bars allows to evaluate this quantity directly from the total length of bars. As it has already been said before, the trusses are externally constrained with a hinge and a trolley, so that the global behavior is analogous to the corresponding simply supported beam. In that way, the influence of large displacements on the internal stress state can be neglected and the linear static analysis is reliable. This fact has been confirmed by some non linear analyses, performed taking into account large displacements. Three different load conditions are used in analysis: vertical uniform at the top, vertical uniform at the bottom and lateral load (Figure 22). The loads are applied as nodal loads and they are calibrated in order to have the same resultant and then to produce the same reactions when they are applied on different trusses. The total vertical load applied at top is 15 KN and at the bottom chord is 15 KN, and the total lateral load applied is 15 KN. All members are hollow tubes having 6 cm diameter and 3 mm thickness made of steel, and the Young’s Modulus of each member is 2.05e + 011 Pa and Poisson’s Ratio is 0.3.
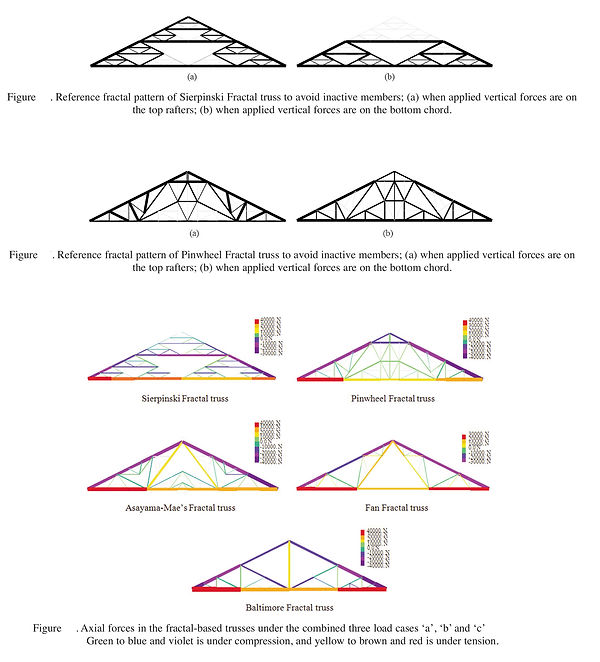
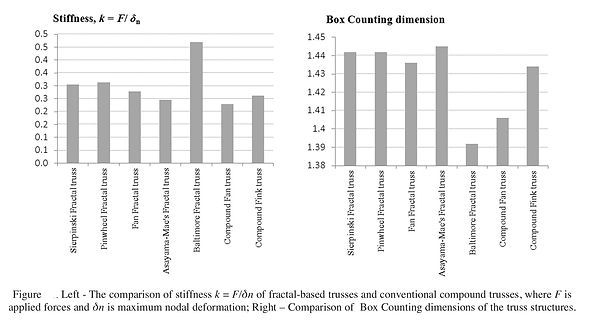
The structural analysis shows that the self-similar fractal branching of trusses is suitable to make them able to carry almost distributed loads, on both the upper inclined rafters and on the bottom chord. The internal forces flows largely depend on the applied load condition and they suggest that new shapes can be derived from the fractal patterns. This is particularly interesting from the architectural point of view, because such new solutions can show aesthetical values and innovative appearance that make them suitable for real design applications. The analysis also informs that the lattice density, as a measure of Box Counting dimension, has no significant influence on the strength of truss structures. It is the truss topology by means of geometric configuration that can offer strength.